使用矩阵乘法进行反向传播误差

此前，我们执行大量计算以得到前馈输入信号时，矩阵乘法帮助了我们。要明白误差反向传播是否可用通过使用矩阵乘法变得更加简洁，让我们使用符合写出步骤。这就是将过程矢量化。

计算的起始点是在神经网络最终层中出现的误差。此时，在输出层，神经网络只有两个节点，因此误差只有${e}_{1},{e}_{2}$。

$${error}_{output}=\begin{pmatrix}{e}_{1}\\{e}_{2}\end{pmatrix}$$

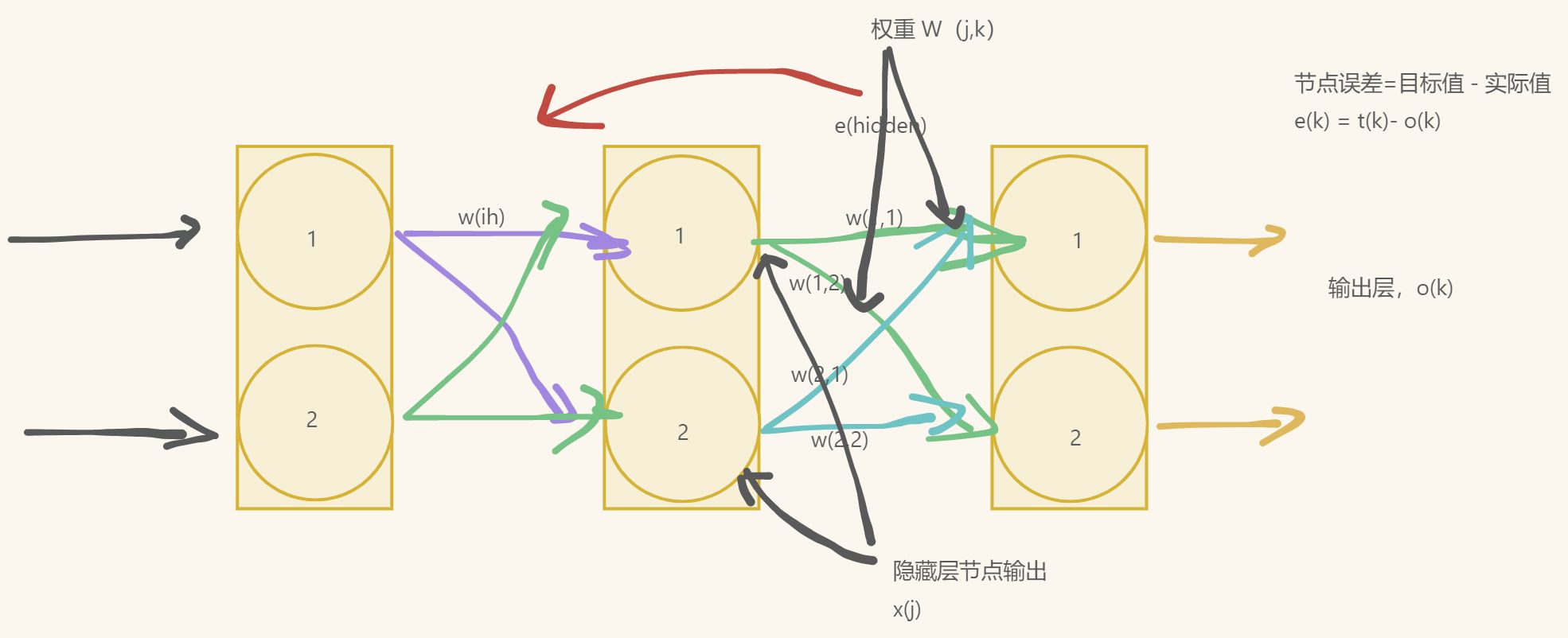
我们需要为隐藏层的误差构建矩阵。假设有两条路

使用梯度下降的方法

首先，让我们展开误差函数，这是对目标值和实际值之差的平方进行求和，这是对所有n个输出节点的和：

$$\frac {\partial E} {\partial {w}_{j,k}}=\frac {\partial } {\partial {w}_{j,k}}\sum _{n} {{({t}_{n}-{o}_{n})}^{2}}$$

此处，我们所做的一切，就是写下实际的误差函数E。 在节点$n$的输出${o}_{n}$只取决于连接到这个节点的链接，因此我们可以直接简化这个表达式。这意味着，由于这些权重是链接到节点$k$的输出不依赖于权重${w}_{j,b}$,其中，由于$b$和$k$之间没用链接，因此$b$与$k$无关联。权重${w}_{j,b}$是连接输出节点$b$的链接去找你，而不是输出节点$k$的链接权重。

这意味着，除了权重${w}_{j,k}$所链接的节点（也就是${o}_{k}$）外，我们可以从和中删除所有的${o}_{n}$,这就完全删除了令人厌恶的求和运算。这是一个很有用的技巧，值得保留下来收入囊中。

这意味着：误差函数不需要对所有节点求和。原因是节点的输出只取决于所连接的链接，就是取决于链接权重。

$$\frac {\partial E} {\partial {w}_{j,k}}=\frac {\partial } {\partial {w}_{j,k}}\ {({t}_{n}-{o}_{n})}^{2}$$

${t}_{k}$的部分是一个常数，因此它不会随着${w}_{j,k}$的变化而变化。也就是说，${t}_{k}$不是${w}_{j,k}$的常数。由于我们使用权重前馈信号，得到输出值${o}_{k}$，因此这个表达式留下了我们所知的依赖于${w}_{j,k}$的${o}_{k}$,因此这个表达式留下了我们所知的依赖于${w}_{j,k}$的${o}_{k}$的部分。

使用联社法则，将这个微积分任务分解成更多易于管理的小块。

$$\frac {\partial E} {\partial {w}_{j,k}}=\frac {\partial E} {\partial {o}_{k}}\cdot \frac {\partial {o}_{k}} {\partial {w}_{j,k}}$$ 现在，我们可以反过来对相对简单的部分各个击破。我们对平方函数进行简单的微分，就很容易击破了第一个简单的项。这使得我们得到了一下式子：

$$\frac {\partial E} {\partial {w}_{j,k}}=-2({t}_{k}-{o}_{k})\cdot \frac {\partial {o}_{k}} {\partial {w}_{j,k}}$$

对于第二项，我们需要仔细考虑一下，但是无需考虑过久。${o}_{k}$是节点$k$的输出，如果你还记得，这是在连接输入信号上进行加权求和，在所得到结果上应用$S$函数得到的结果。让我们将这写下来，清楚地表达出来。

$$\frac {\partial E} {\partial {w}_{j,k}}=-2({t}_{k}-{o}_{k})\cdot \frac {\partial } {\partial {w}_{j,k}}sigmoid(\sum _{j}{{w}_{j,k}\cdot {o}_{j})}$$

${o}_{j}$是前一个隐藏层节点的输出，而不是最终层的输出${o}_{k}$。

我们如何微分$S$函数呢？使用微积分对$S$函数求微分，这对我们而言是一种非常艰辛的方法，但是，其他人已经完成了这项工作。我们可以只使用众所周知的答案，就像全世界的数学家每天都在做的事情一样。

$$\frac {\partial } {\partial x}sigmoid(x)=sigmoid(x)(1-sigmoid(x))$$

在微分后，一些函数变成了非常可怕的表达式。$S$函数微分后，可以得到一个非常简单、易于使用的结果。在神经网络中，这是$S$成为大受欢迎的激活函数的一个重要原因。 因此，让我们应用这个酷炫的结果，得到一下的表达式。

$$\frac {\partial E} {\partial {w}_{j,k}}=-2({t}_{k}-{o}_{k})\cdot sigmoid(\sum _{j} {{w}_{j,k}}\cdot {o}_{j})(1-sigmoid(\sum _{j} {{w}_{j,k}}\cdot {o}_{j}))\cdot \frac {\partial } {\partial {w}_{j,k}}(\sum _{k} {{w}_{j,k}}\cdot {o}_{j})$$

$$=-2({t}_{k}-{o}_{k})\cdot sigmoid(\sum _{j} {{w}_{j,k}}\cdot {o}_{j})(1-sigmoid(\sum _{j} {{w}_{j,k}}\cdot {o}_{j}))\cdot {o}_{j}$$

这个额外的最后一项是什么呢？由于在$sigmoid()$函数内部的表达式也需要对${w}_{j,k}$进行微分，因此我们对$S$函数微分项再次应用链式法则。这也非常容易，答案很简单，为${o}_{j}。$

在写下最后的答案之前，让我们把在前面的2去掉。我们只对误差函数的斜率方向感兴趣，这样我们就可以使用梯度下降的方法，因此可以去掉2.只要我们牢牢记住需要什么，在表达式前面的常数，无论是2、3还是100，都无关紧要。因此，去掉这个常数，让事情变得简单。

这就是我们一直在努力要得到的最后答案，这个表达式描述了误差函数的斜率，这样我们就可以调整权重${w}_{j,k}$了。

$$\frac {\partial E} {\partial {w}_{j,k}}=-({t}_{k}-{o}_{k})\cdot sigmoid(\sum _{j} {{w}_{j,k}}\cdot {o}_{j})(1-sigmoid(\sum _{j} {{w}_{j,k}}\cdot {o}_{j}))\cdot {o}_{j}$$

这就是我们一直在寻找的神奇表达式，也是训练神经网络的关键。

$-({t}_{k}-{o}_{k})$就是（目标值-实际值），我们对此已经很清楚了。在$sigmoid$中的求和表达式也很简单，就是进入最后一层节点的信号，我们可以称之为${i}_{k}$,这样它看起来比较简单。这是应用激活函数之前，进入节点的信号。最后一部分是前一隐藏节点$j$的输出。

我们还需要做最后一件事情。我们所得到的这个表达式，是为了优化隐藏层和输出层之间的权重。现在，我们需要完成工作，为输入层和隐藏层之间的权重找到类似的误差斜率。

我们可以简单地使用刚才所做的解释，为感兴趣的新权重集重新构建一个表达式。

• 第一部分的（目标值-实际值）误差，现在变成了隐藏层节点中重组的向后传播误差，正如在前面所看到的那样。我们称之为${e}_{j}$。
• $sigmoid$部分可以保持不变，但是内部的求和表达式指的是前一层，因此求和的范围是所有由权重调节的进入隐藏层节点$j$的输入。我们可以称之为${i}_{j}$。
• 现在，最后一部分是第一层节点的输出${o}_{i}$，这碰巧是输入型号。

这种巧妙的方法，简单利用问题中的对称性构建了一个新的表达式，避免了大量的工作。这种方法虽然很简单，但却是一种很强大的技术，一些天赋异禀的数学家和科学家都使用这种技术。你肯定可以使用这个技术，给你的队友留下深刻印象。

因此，我们一直在努力达成的最终答案的第二部分如下所示，这是我们所得误差函数斜率，用于输入层和隐藏层之间权重调整。

$$\frac {\partial E} {\partial {w}_{i,j}}=-({e}_{j})\cdot sigmoid(\sum _{i} {{w}_{i,j}}\cdot {o}_{i})(1-sigmoid(\sum _{i} {{w}_{ij}}\cdot {o}_{i}))\cdot {o}_{i}$$

现在，我们得到了关于斜率的所有关键的神奇表达式，可以使用这些表达式，在应用每层训练样本后，更新权重，在接下来的内容中我们将会看到这一点。

记住权重改变的方向与梯度方向相反，正如我们在先前的图中清楚看到的一样。我们使用学习因子，调节变化，我们可以根据特定的问题，调整这个学校因子。当我们建立线性分类器，作为避免被错误的训练样本拉得太远的一种方式，同时也为了保证权重不会由于持续的超调而在最小值附件来回摆动，我们都发现了这个学校因子。让我们用数学的形式来表达这个因子。

$$new{\, w}_{j,k}\, =\, old\, {w}_{j,k}-\propto \cdot \frac {\partial E} {\partial {w}_{j,k}}$$

更新后的权重${w}_{j,k}$是由刚刚得到误差斜率取反来调整旧的权重而得到的。正如我们先前所看到的，如果斜率为正，我们希望减小权重，如果斜率为负，我们希望增加权重，因此，我们要对斜率取反。符号$\propto$是一个因子，这个因子可以调节这些变化的强度，确保不会超调。我们通常称这个因子为学习率。

这个表达式不仅适用于隐藏层和输出层之间的权重，而且适用于输入层和隐藏层之间的权重。差值就是误差梯度，我们可以使用上述两个表达式来计算这个误差梯度。

由于学习率只是一个常数，并没有真正改变如何组织矩阵乘法，因此我们省略了学习率$\alpha$。

权重改变矩阵中包含的值，这些值可以调整链接权重${w}_{j,k}$，这个权重链接了当前层节点$j$与下一层节点$k$。你可以发现，表达式中的第一项使用下一层（节点$k$）的值，最后一项使用前一层（节点$j$）的值。

因此，权重更新有如下矩阵形式，这种形式可以让我们通过计算机编程语言高效地实现矩阵运算。

$$\Delta {w}_{j,k}=\propto \cdot {E}_{k}\cdot {O}_{k}(1-{O}_{k})\cdot {{O}_{j}}^{T}$$

实际上，这不是什么复杂的表达式。由于我们简化了节点输出${O}_{k}$,那些sigmoids已经消失了。 好了！任务完成。

关键点

• 神经网络的误差是内部链接权重的函数。
• 改进神经网络，意味着通过改变权重减少这种误差。
• 直接选择合适的权重太难了。另一种方法是，通过误差函数的梯度下降，采取小步长，迭代地改进权重。所迈出的每一步的方向都是在当前位置向下斜率最大的方向，这就是所谓的梯度下降。
• 使用微积分可以很容易地计算出误差斜率。

权重跟新成功范例

我们来演示几个有数组的示例，让读者看看这种权重更新的方法是可以成功的。 下面的网络是我们之前演示过的一个，但是这次，我们添加了隐藏层第一个节点${O}_{j=1}$和隐藏层第二个节点${O}_{j=2}$的示例输出值。这些数字只是为了详细说明这个方法而随意列举的，读者不能通过输入层前馈信号正确计算得到它们。

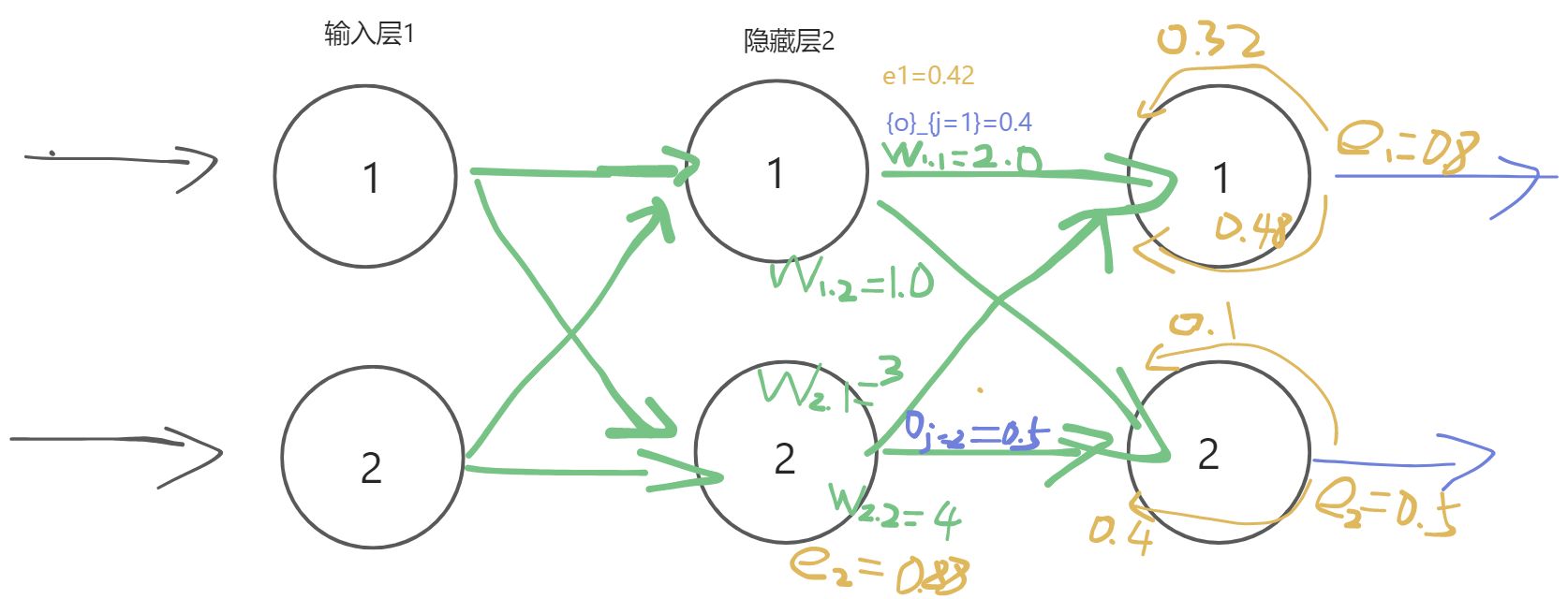我们要更新隐藏层和输出层之间的权重${w}_{1.1}$。当前，这个值为2.0. 让我们再次写出误差斜率。

$$\frac {\partial E} {\partial {w}_{j,k}}=-({t}_{k}-{o}_{k})\cdot sigmoid(\sum _{j} {{w}_{j,k}}\cdot {o}_{j})(1-sigmoid(\sum _{j} {{w}_{j,k}}\cdot {o}_{j}))\cdot {o}_{j}$$

让我们一项一项地进行运算：

• 第一项$({t}_{k}-{o}_{k})$得到误差
• S函数内的求和为$\sum _{j} {{w}_{j,k}}\cdot {o}_{j}$为$(2.0 \times 0.4 )+( 3.0 * 0.5)=2.3$
• $sigmoid(1/(1+{e}^{-2.3}))$为0.999。中间的表达式为$0.909*(1-0.909)=0.083$
• 由于我们感兴趣的是权重${w}_{1.1}$，其中$j=1$，因此最后一项${o}_{j}$也很简单，也就是${o}_{j=1}$。此处，${o}_{j}$值就是0.4。

将这三项相乘，同时不要忘记表达式前的负号，最后我们得到-0.00265。 如果学习率为0.1，那么得出的该变量为$-(0.1*-0.02650)=+0.002650$。

因此，新的${w}_{1.1}$就是原来的2.0加上0.00265等于2.00265。 虽然这是一个相当小的变化量，但权重经过成百上千次1的迭代，最终会确定下来，达到一种布局，这样训练有素的神经网络就会生成与训练样本中相同的输出。